The Geometric Mean Expansion of Space
We argue that the universe is undergoing a geometric mean expansion. In the hyperverse model, the universe is the surface volume of an expanding, four dimensional, hollow, 'hypersphere'. The observable universe, which is a tiny part of the surface of the whole hyperverse, acts, in many ways, as though it is a stand-alone hyperverse, and this is due to the effects of time-scaling.
The hyperverse surface is viewed as consisting of 4D vortices, and is one vortex thick, as explained the time paper. Expansion is the radial advance of the surface vortices, and can be viewed as a radially advancing 'front'. It appears that the vortices are shrinking with expansion, and the shrinkage is of a geometric mean character. Consider the balloon analogy used to represent the expansion of space. As the balloon expands, its surface area increases, but the thickness of the latex decreases. The expansion of space appears to be somewhat like this. The larger the radius of the hyperverse, the smaller is the radius of the surface 4D vortices. This results in more, and smaller, vortices. Energy appears to be a function of the radius. Shrinking a surface vortex radius by one-half results in four times as many vortices, each with an energy of one-half the original resulting in a doubling of the total energy. This idea appears to be the core process behind the increase in the energy of the universe resulting from expansion.
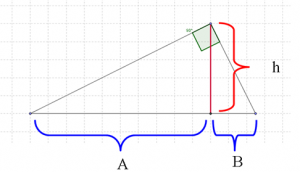
A common way to display the geometric mean is by the use of a right triangle. The product of side A and side B equals 'h', the height, squared. As side A is increased, side B gets smaller, while the height stays the same size.
The Planck Values are the Geometric Means of Expansion
The geometric mean expansion of space gives us a simple explanation for the Planck values, which pop up commonly in cosmology and physics. The Planck mass and energy are rather large values, whereas the Planck length and Planck time are very small. Planck values have no known physical significance. The model of the hyperverse, undergoing a geometric mean expansion, says that the Planck values are the initial values of the universe, telling us what the universe was like when expansion started. The Planck values are preserved as geometric means of the large (hyperverse as a whole) and the small (the surface vortices).
The Geometric Mean Expansion of Space Creates Quanta
This gives us a simple way to create a universe from nothing... because the universe actually comes from itself. Quanta appear to exist as a result of, the cause of, the geometric mean expansion of space. We find that the geometric mean expansion creates two levels, or scales, of quanta, both small. One works out to be the quanta of our quantum mechanics, while the other is much, much smaller. A geometric mean expansion gives us a simple way to explain the expansion of space and the creation of energy. It is not a universe from nothing, but a universe from itself. And the existence of quanta is a result of, or the cause of, the expansion.
Details are explained in the paper, "A Universe From Itself: The Geometric Mean Expansion of Space and the Creation of Quanta".