The Basis of Electrical Attraction and Repulsion
If space is composed of 'atoms of space', and these atoms of space have spin, we can combine them to create units of matter that have electrical charges that match what we see with elementary particles. This simple system explains fractional charges and antimatter.
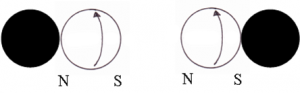
In the following figures, we define the black sphere as the center, or point of attraction, and the white sphere as the atom of space. The atom of space has spin. If opposite poles face each other, we have attraction, as shown in Figure 1. If similar poles are facing each other, the spins would not mesh, but repel, as shown in Figure 2.
Figure 1: Attraction. When opposite poles face each other, they can unite in their spin. This is attraction.
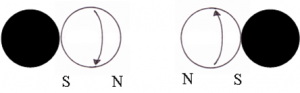
Figure 2: Repulsion. When the same poles face each other, spin is opposed, and the units would be repelled from one another. This is repulsion.
Six Sides per Particle
If we allow each particle to have six sides, or points of attachment, we get:
Six sides per particle gives us six bound orientations.
From this, to make drawing easier, we can place all six atoms of space in a 2D representation, as such:
A 2D representation of the 3D arrangement.
Notation
We can create a notation for these arrangements to allow us to use a text-based description of the arrangements.
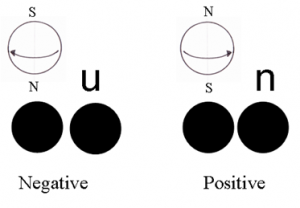
The black spheres, or circles, represent the particle centers. In the 'Negative' example, the north faces the center and it is the south pole that faces outwards. We will use the letter 'u' to represent a negative orientation. In the 'Positive' example, the south pole faces the center, and it is the north pole that faces outwards. We will represent this orientation with an 'n'.
Fractional Charges, Particles, and Anti-Particles
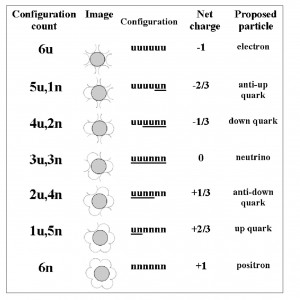
We find that if six atoms of space are assembled to form a particle, we can create all the elementary particle charge relationships. A full charge, of negative one, occurs when all six of the bound quanta, or atoms of space, are oriented so that their negative poles face outwards. If five face outwards, and one inwards, then we have a net of four of six facing outwards. This would give us a net charge of minus two-thirds, corresponding to an anti-up quark. The following table gives the arrangements, charges, and associated particles.
With the 'nu' notation, we have underlined the pairs of spin that cancel each other, allowing for a more rapid assessment of the net charge of the particles.
Table 1. A list of all the combinations of six orientations of the quanta of space surrounding the center. This produces all the known electrical charge arrangements of elementary particles. Click on the table to see it more clearly.
This system gives us all the known electrical charges, explains fractional charges, and produces the anti-particles.
Particle Annihilation
We can use the model to explain particle-antiparticle annihilation. IN this example, we place an electron near a positron, and we find that all six quanta of either particle are able to bind to, and attract each quanta of the other. There is nothing to stop them from pulling together fully.
When a particle meets its antiparticle, all the quanta are able to unite and pull together. There is nothing to stop the particles from being pulled together.
We would find that combining all pairs of particles and their anti-particle will result in annihilation due to unrestrained attraction.
Building the Neutron
We can use our particle model to construct protons and neutrons. Let us start with the neutron.
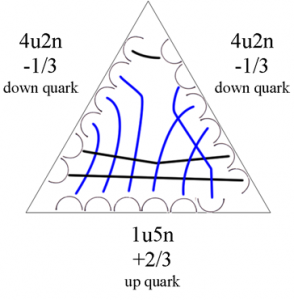
By combining two down quarks and one up quark, we get the neutron. All the component quanta, within the system of three, are cancelled. Notice that no two quarks can fully attract, or repel another. The system of three quarks gives a neutral charge. The 'nu' notation is 9n9u; all components cancel.
Building the Proton
We can construct the proton using three quarks:
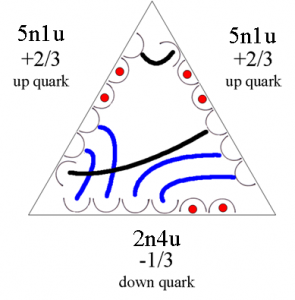
The 'nu' notation of the proton is 12n6u. It leaves a net of six unmatched positive quanta, for a net charge of plus one, just right to bind to an electron.
The proton has a hidden full negative charge, and this is why the electron is not fully pulled into the proton.
The model predicts the proton has hidden negative charge. The 'nu' notation of 12n6u says that there are six negatively oriented quanta within the proton. Even though they are canceled out, they still exist. The six negatively oriented quanta are present, and would prevent the electron from being fully pulled into the proton. We have simultaneous attraction and repulsion of the electron by the proton. Twelve quanta attract, and six repel.
The model predicts the dark matter particle.
The condensation neutrino is probably the dark matter particle. Click here.
The above materials are in this paper.
The Point of Attraction
In the above description of elementary particle structure, we speak of a "point of attraction". In pursuing the concepts presented on this website, the 'ideal particle' was discovered, explained in this paper, and on this page. The ideal particle appears to represent the target the expanding universe is aiming for in particle creation. Actual particles presumably vary from the ideal due to the effects of the various spin orientations into which they can assemble.
The ideal particle concept gives us a working tool to calculate the effects of expansion and time on particle mass, radius and number. What we see is that particles are not static entities, but their mass and radius change with expansion, and the number of particles also increases as the universe grows.
And the argument is made, in the matter and gravity paper, that particles exist to conserve the angular momentum of the expanding universe. This is not a one-time act, something a particle can do and then stop doing. The angular momentum of the hyperverse continually increases, and thus particles of matter must continually accrete the quanta of space in order to conserve angular momentum.
The "point of attraction" is simply the center of the particle.
Overall, this model gives a simple basis for the electrical structure of elementary particles, explaining fractional charge and anti-particles.